Data Structure and Algorithms - Stack
A stack is an Abstract Data Type (ADT), that is popularly used in most programming languages. It is named stack because it has the similar operations as the real-world stacks, for example – a pack of cards or a pile of plates, etc.

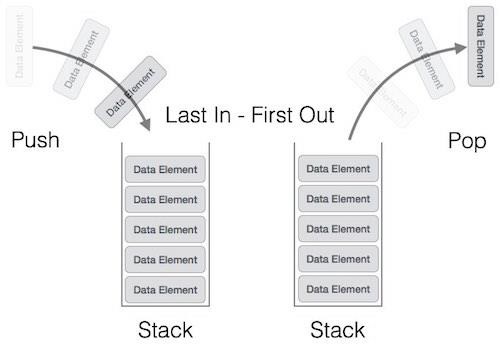
The stack follows the LIFO (Last in - First out) structure where the last element inserted would be the first element deleted.
Stack Representation
A Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack.
The following diagram depicts a stack and its operations −
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.
Basic Operations on Stacks
Stack operations usually are performed for initialization, usage and, de-initialization of the stack ADT.
The most fundamental operations in the stack ADT include: push(), pop(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the stack.
Stack uses pointers that always point to the topmost element within the stack, hence called as the top pointer.
Working of Stack
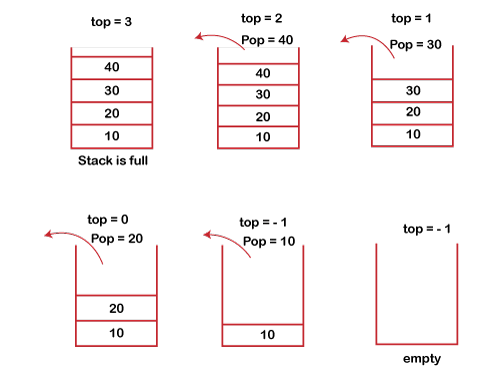
Stack works on the LIFO pattern. As we can observe in the below figure there are five memory blocks in the stack; therefore, the size of the stack is 5.
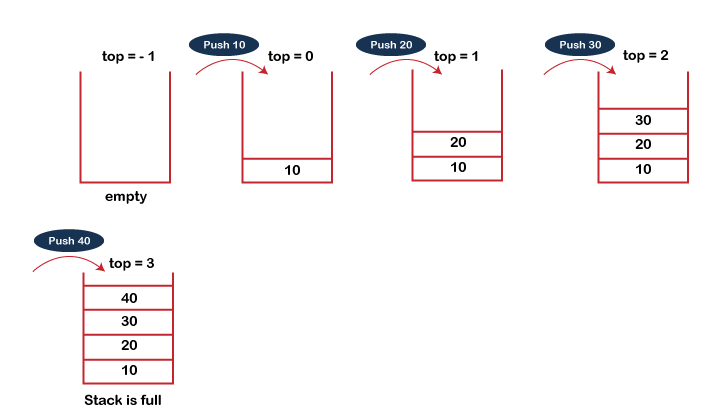
Suppose we want to store the elements in a stack and let's assume that stack is empty. We have taken the stack of size 5 as shown below in which we are pushing the elements one by one until the stack becomes full.
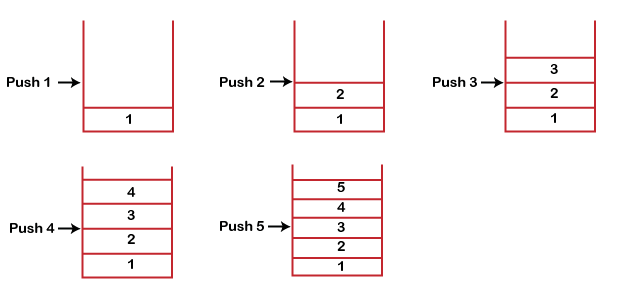
PUSH operation
The steps involved in the PUSH operation is given below:
- Before inserting an element in a stack, we check whether the stack is full.
- If we try to insert the element in a stack, and the stack is full, then the overflow condition occurs.
- When we initialize a stack, we set the value of top as -1 to check that the stack is empty.
- When the new element is pushed in a stack, first, the value of the top gets incremented, i.e., top=top+1, and the element will be placed at the new position of the top.
- The elements will be inserted until we reach the max size of the stack.
POP operation
The steps involved in the POP operation is given below:
- Before deleting the element from the stack, we check whether the stack is empty.
- If we try to delete the element from the empty stack, then the underflow condition occurs.
- If the stack is not empty, we first access the element which is pointed by the top
- Once the pop operation is performed, the top is decremented by 1, i.e., top=top-1.